中学受験・算数、苦手な立体図形の「切断」問題、スタートは家庭内での対話が重要？

その２「切断」

　前回に引き続き、今回も「立体図形」を扱っていきたいと思います。前回は“展開図”をテーマにしましたが、今回は“切断”がテーマです。前回の記事の中で“見取り図”を描写してもらったエピソードがありましたが、この“切断”においても必ずといっていいほど以下のようなエピソードが出てきます。

“切断”とは何か？等、全く伝えることなしに描いてもらうと、多くの子供たちが以下のような線を描きます。

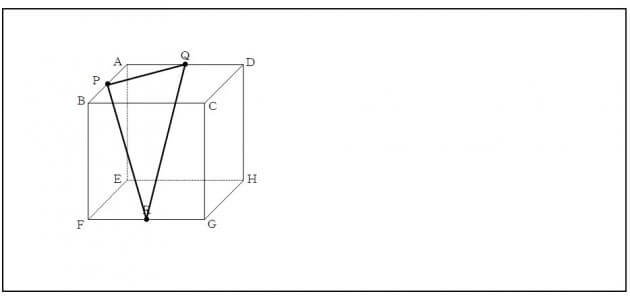
　前回の“見取り図”でも感じたことですが、ここでも実際の“モノ”を見たり扱ったりといったことが少なかったんだろうなあと感じます。中には何も伝えることなしに正解の“切り口”を描ける子もいましたが、聞いてみると、

「家でお手伝いした時に“豆腐”を切ってみたよ！」

「“発泡スチロール”の立方体が売っていたから、それを切ってみたことある！」

といった返事が返ってきました（今は便利な“モノ”が売っていますね）。

　やはり実際に見たり扱ったりすることは大事なんだなあと感じる反面、“想像”だけでは厳しいものがありますね。そもそも“切断”することが何であるか実際に“切り離す”場面を見たことがないのであればなおさらです。まずは“見る”“扱う”という前提があった上で、ここでも“手順・方法”を学んでほしいと思います。

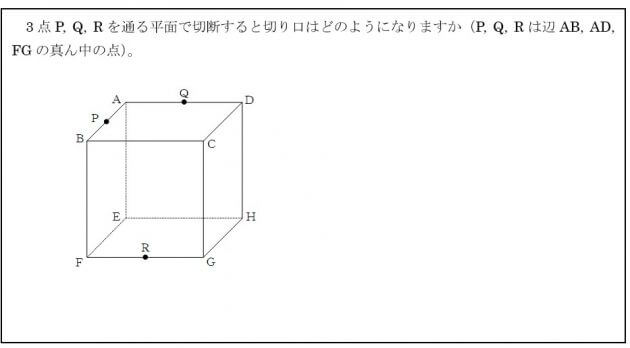
【手順１】同一平面上の２点を結ぶ

　上の面（面ABCD）におけるPとQは“同一平面上の２点”にあたるので一直線に結びます。“切り口”とは立体の表面上における線を結んだものなので、PとR, QとRは立方体の表面上の線ではないため結んではいけませんね（“串”を貫通させたようなものです）。

【手順２】向かい合った（平行な）面に平行線を引く

　平行な２つの平面をもう一つの平面で切ると、２つの面には平行な切り口の線がつきますね（以下のようなイメージ）。

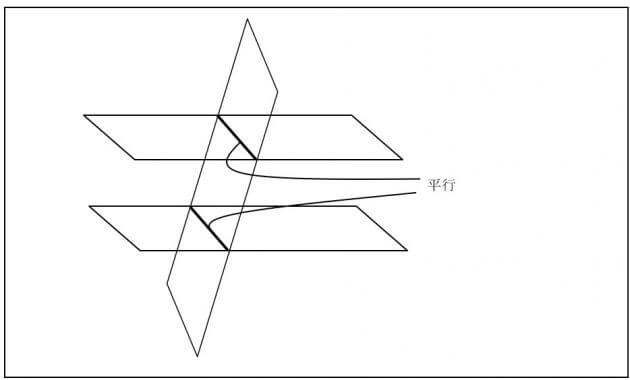
　上の面（面ABCD）と下の面（面EFGH）が向かい合った（平行な）面ですから、PQと平行になるようにRから平行線を引くと以下のようになります。

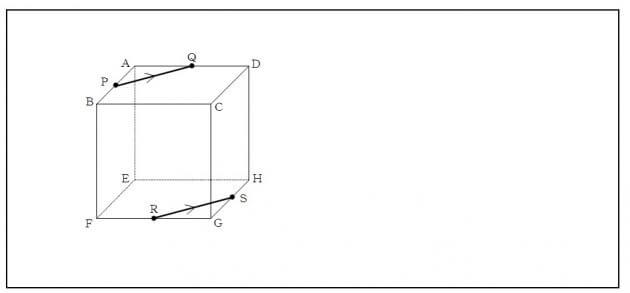
【手順３】線を延長して、新たな交点をつくる

　一つの平面で切断するということは、その面を拡張した時にぶつかった交点も一つの平面上にあるということですね。以下のように線（RS）を延長してみましょう。

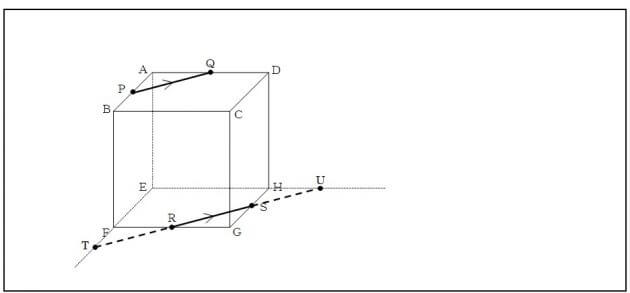
　RSを延長してできた交点TはPと、交点UはQと同一平面上の２点となりましたね。よって【手順１】に戻って以下のように結びます。

　さらに立方体の辺上にできた交点VとRが、交点WとSが同一平面上の２点となりましたので、【手順１】のとおり結びます。

　上の図のように“切り口”の線はしっかり立方体の表面上に引かれていなければいけません（そもそも“切断”できませんね）。ここでは“切り口”の形は正六角形となりました。

“想像”だけで“意味・理屈”をつかむことなく感覚で行うのではなく、しっかり“手順・方法”を利用することはこの“切断”においても大切ですね。また是非実際の“モノ”を用意して、本当にそのようになっているのか確認してほしいと思います。

　次は以下のような“積み木の切断”です。

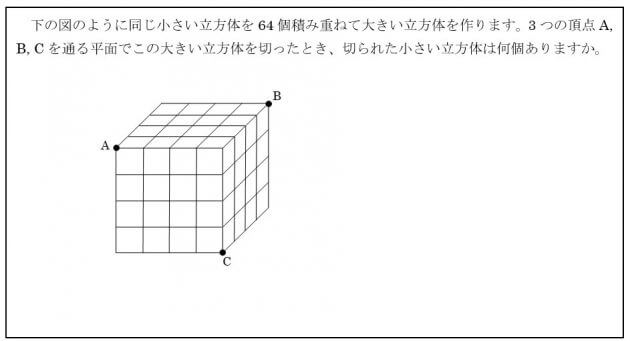
　まずは大きな立方体の“切り口”となる線を引いてみます。【手順１】を利用して以下のような線が引けますね。

　大きな立方体における“切り口”は判明しましたが、内側にも積み重なっている小さい立方体がどれだけ切られているかはわかりにくいですね。内部はこんな状態かなと以下のような線を引いてみても確信がもてません。

　そこで以下のように段ごとに“スライス”してみましょう。

　１段目ではABが切断の入り口とすると、アイが出口となりますね。「○」のついた７個の小さい立方体が切られたことになります。２段目はアイが入り口、ウエが出口となり、５個の小さい立方体が切られています。３段目、４段目は以下のとおりです。

“切り口”の形だけではなく、段ごとに“スライス”することによって内部の状況を把握することができました。

“切り口の手順”も“スライス”も“モノ”が手元にない状態で想像だけに頼らない便利な“手順・方法”です。今では定番となっている“手順・方法”ですが、この基本は様々な応用問題に活かすことができます（“多段階切断”“積み木のくり抜き”等）。いずれ実際の「入試問題」をご紹介する中でも扱っていくことになると思います。

　ここまで２回にわたって「立体図形」を扱ってきました。共通して言えることは、最初のスタートはやはり実際の“モノ”を見たり扱ったりすることが大切であることです。以前の記事の中でも“生活”“対話”の中で自然と身につく数的感覚の話を記しましたが、こういった図形においても是非ご一緒に見たり扱ったりしてあげてください。その後問題に取り組んだ際には、“意味・理屈”をしっかりつかんだ上で“手順・方法”を利用してほしいと思います。

（文＝内田実人／中学受験指導スタジオキャンパス）