新型コロナ、「指数関数的増加」が終息するポイント…3月末から再び指数関数の経路

　新型コロナウィルスへの感染の拡大が世界中を震撼させています。読者の皆さんはすでに「感染者の指数関数的増加」ということばを何度も目にしているのではないでしょうか。これは、ビジネスでもときどき使われる表現です。「売上が倍々ゲームで増える」「借金が（複利により）雪だるま式に増える」というのは、いずれも指数関数的増加のケースです。要は、何らかの変数が一定の倍率で増えていく場合、それは指数関数的増加と呼ばれます。

　では、指数関数とは何か、ビジネスにどう関係するのかと少し興味を持たれた方は、ぜひ以下の文をお読み下さい。

　新型コロナウィルスへの感染者から売上でも借金でも、指数関数的な変化が起きると、日常の線形的感覚では追いつけなくなります。それがまさに、新型コロナウィルス感染症をめぐって、少なからぬ人々が直面している問題でもあります。この記事では、まずは新型コロナウィルスの感染拡大を題材に指数関数的変化をどう捉えるかを説明し、それがどのように終息するかについても言及します。

新型コロナウィルスの感染は指数関数的に増加した

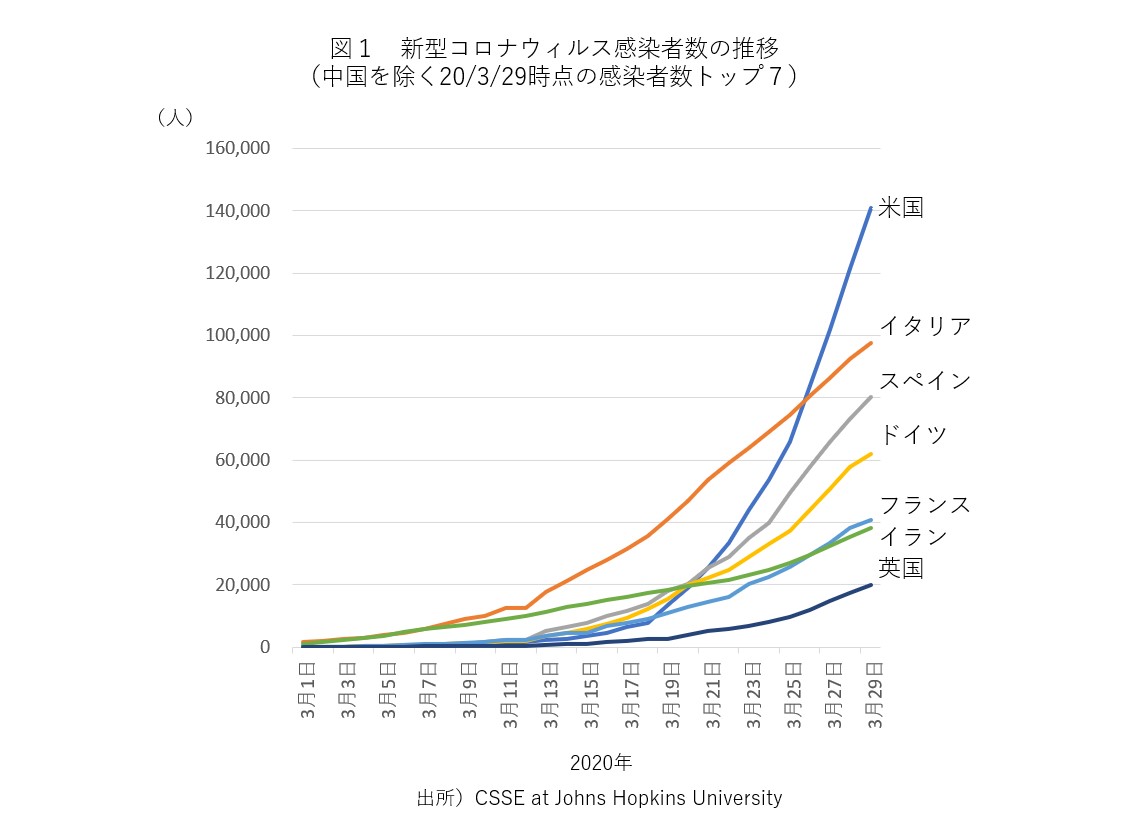
　図1には、2020年3月に入ってから感染が急拡大した、中国を除く主要国での新型コロナウィルスへの感染者数の推移が描かれています（データは米国のジョンズ・ホプキンス大学のサイトから入手）。ここでいう「感染者数」とは、その時点までに感染が確認された人の数で、すでに回復した人や亡くなった人の数も含んでいます。この図をひと目見てわかるように、最初はゆるやかであった感染者の増大が、時間とともに加速しています。たとえば米国での感染者数は、3月中旬には欧州の国々を下回っていたのに、3月末には世界でトップに躍り出ました。

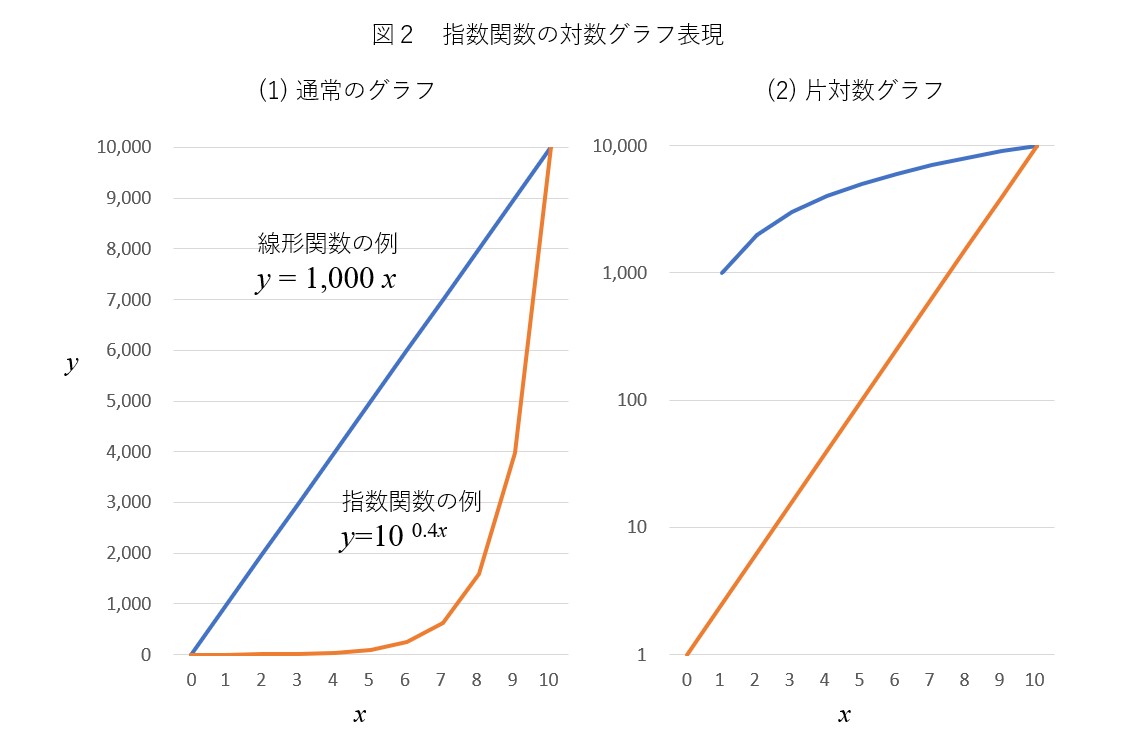
　上で「指数関数的変化」とは倍率が一定の変化である、と書きました。つまり、ある会社の売上が毎年同じ％で増加しているなら、それは指数関数的な増加ということになります。経営者が当社は去年売上が5％成長したから、今年も同様に5％成長したいという目標を掲げることはよくあると思います。ただし、その目標が達成されるためには、売上の増加分が昨年以上に大きくならなくてはなりません（図2(1)の赤線で示された指数関数）。一方、毎年の増加分が同じだと図2(1)の青線で示された線形関数になります。

　このグラフの縦軸を対数目盛に変換したものは、片対数グラフと呼ばれています。対数目盛とは、図2(2)の縦軸を見ればわかるように、ふつうの目盛と違って1→10→100→1,000→10,000…と1目盛ごとに10倍ずつ値が増えていくものです（つまり数字が大きくなるほど圧縮されて表示されると解釈できます）。

　何でわざわざそんな変わったグラフを使うかというと、指数関数をこのグラフの上に描くと直線になり、その傾きは関心を持っている変数の増加率（成長率）になるからです（その理由はここでは省略します）。

　逆にいえば、片対数グラフに変化をプロットしたら直線になった場合、その変化は指数関数的で、その傾きが増加率（成長率）を表していることになります。これは大変便利なので、Excelのグラフにもワンクリックでふつうの目盛を対数目盛に変換できる機能がついているわけです。なお、ふつうのグラフの上では直線的であった変化（青線）は、片対数グラフ上では曲線になり、傾きがだんだん小さくなっています。すなわち、分母が大きくなるのに分子が一定ですから、当然成長率は低下していきます。

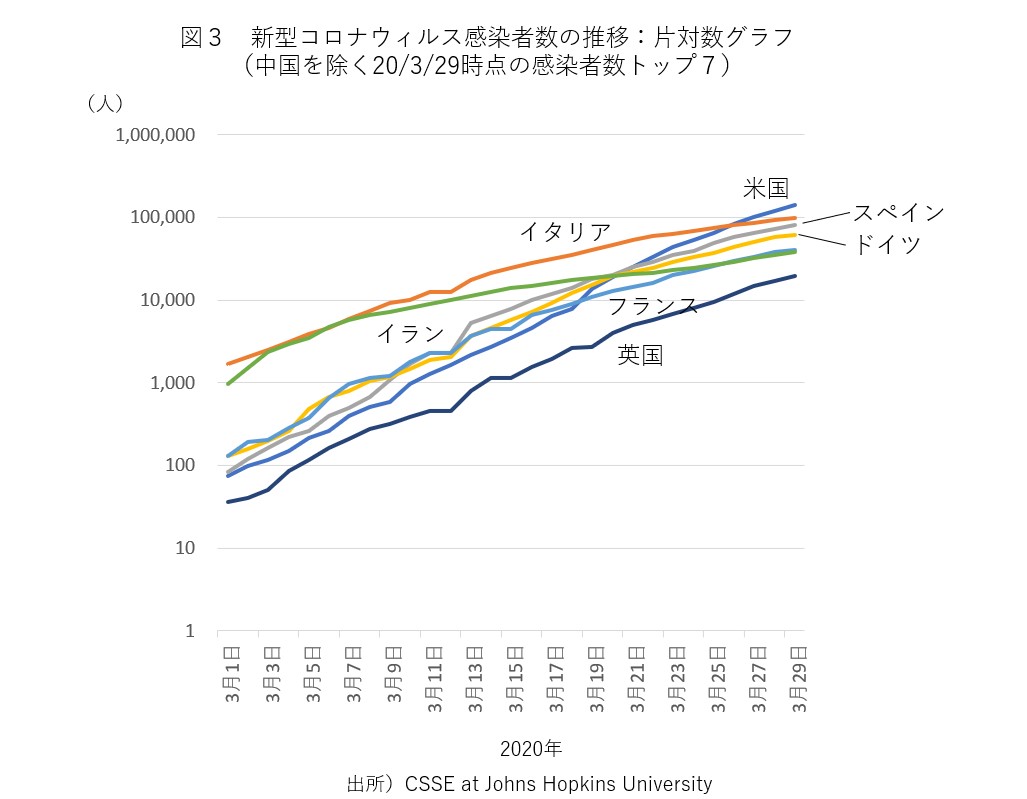
　そこで図1を片対数グラフに変換すると、図3のようになります。多くの国について、感染者数の変化は直線上に乗っているように見えますので、おおまかにいえば指数関数的増加であったといえます。ただし、イタリアやイランは3月上旬に比べ後半は傾きがわずかに小さくなってきているので、新たな感染者数が減少しつつあり、指数関数的増加とは違う局面に入った可能性があります。

感染はなぜ指数関数的に増加するのか、そしていつ止まるのか

　感染者数の指数関数的増加の背後には、次のような単純なメカニズムを想定できます。それは、すでに感染した1人が、毎期一定数（αとする）の新たな感染者を生み出す、というプロセスが繰り返されるというものです。これは

[感染者の増分]　＝　α× [これまでの感染者数],  α＞ 0

という方程式で表されます。この式を変形すると、以下のような指数関数になります。

　[ｔ期の感染者数]　＝　β×[10の(α・ｔ)乗],   α, β> 0

　なお、この式では、いったん感染した人は亡くなることも回復することもなく新たな感染者を生み続けること、また免疫をつくることで感染されなくなる人はいないこと、などが仮定されています。したがって、感染症が蔓延し始める時期にはあてはまるものの、ある程度時間が経つと、現実にはフィットしなくなります（そうでないと、あっという間に全人口が感染してしまいます）。

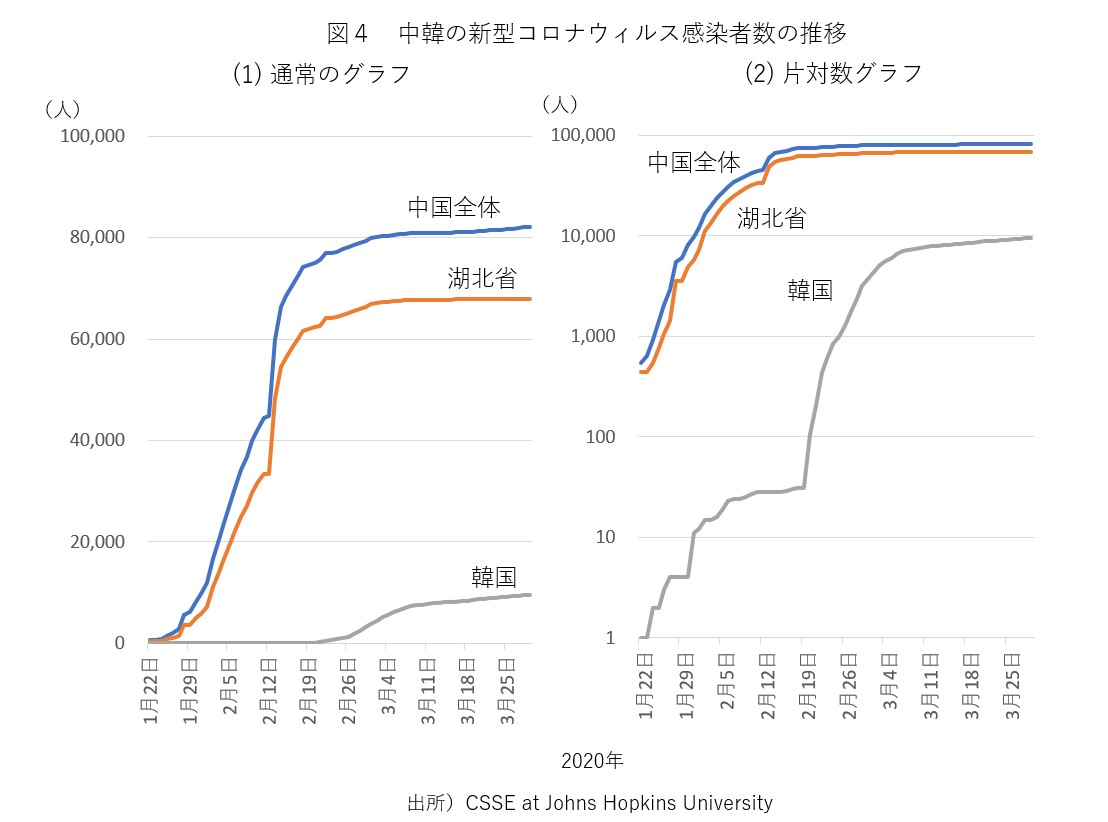
　そこで新型コロナウィルスへの感染が最初に発生したとされる中国、そして次いで感染が急拡大した韓国の例を見てみましょう。図4からわかるように、いずれの国でも、初期には指数関数的増加が起きているものの、あるポイント（変曲点といいます）を超えると増加率が低下し始めて、現在では感染者数がほとんど増えない（つまり新たな感染者がほとんど現れない）状態に達しています。したがって、時間で見た感染者数はS字型のカーブに沿って推移していることがわかります。なお、武漢を含む湖北省のデータにガタツキが見られるのは、感染の基準が途中で変更されたからのようです（奥村晴彦氏のサイトによる）。

　感染者の増加が最終的にS字型カーブになる（どこかで上限に収束する）のは、各国が行った感染者を隔離したり、一般人の移動や集まりを制限したりする措置のためだけではありません。一度感染した人には免疫ができて感染しなくなることが、感染拡大を減速させる最終的な要因になっているのです。このことを考えると、上に書いた方程式は、以下のように修正されることになります。

[感染者の増分]　＝　β× [これまでの感染者数] × [これまでの未感染者数],  β ＞ 0

　つまり、感染者が多いほど新たな感染者が増えるというルールは指数関数の場合と同じですが、それはあくまで未感染者（今後感染する可能性のある免疫のない者）の間でだけ起きる、というルールを加えたのです。未感染者の数は感染者が増えた分だけ減っていきますから、いずれ感染者の増加にブレーキが効き始めるポイント、つまり変曲点が来るわけです。

　この方程式は「ロジスティック関数」といわれています。最終的にこの関数にそって変化するのであれば最初からそれを適用したいところですが、感染の上限となる潜在的感染者（現在の感染者数と未感染者数の合計）の人口が、ある程度時間が経たないと見通せないという問題があります。ロジスティック関数はマーケティングでもよく使われるので、今後、この連載でも紹介していきたいと思います。

日本では、いつ新型コロナウィルスの感染は終息するか

　最後に、日本における新型コロナウィルスへの感染者数の推移を見ることにしましょう（図5）。1月から3月までの変化を見ると、指数関数にしたがっていることが一目瞭然です。片対数グラフに示された線の傾きは少しガタガタしており、増加率が上がったり下がったりしています（分析対象となる感染者数が少ないのでやむを得ません）。3月の中旬に少し傾きが小さくなり、変曲点を越えてS字型カーブの後半へ移行するかと期待されたのですが、3月末に再び上向いて指数関数の経路に戻っています。3月中旬の減速はノイズで、実はずっと指数関数的増加が続いていたのか、新たな指数関数的増加の局面に入ったのかは私にはわかりません。

　今後、感染者数がどう推移するかは、3月末の時点ではまったく不確実です。片対数グラフ上ではわずかな傾きの変化でも、今後の感染者数の差は非常に大きくなります。いかに感染の爆発を防ぐかについては専門外なのでここでは何も書きませんが、かなり危機意識を持たなくてはならないことは確かです。先行きが不確実であるということは、早めに感染者の増加率が低下するという幸運が起きる可能性もあります。しかし、その場合でも再び指数関数的増加が起きるリスクは残りますから、長い戦いに備える必要があります。

（文＝水野誠／明治大学商学部教授）