結婚＝“幸せ”“不幸せ”拡大システムの幸せ機能が見落とされるワケ～幸せ表明がリスクな国

　次に、結婚による“不幸せ”をどうやって測ればいいか、ということが問題になりました。

　当然ですが、そのようなデータが存在するはずがありません。そこで今回は、離婚裁判に持ち込まれた申し立ての動機の項目と、その比率を用いることにしました（司法統計『性別離婚申し立ての動機別割合の推移（1975-2009）』より）。その比率は、離婚の裁判にまで至らないケースにも適用できると考えたためです。

　今回は、目的も狙いもサンプル数も何もかもが違う2つの種類のデータを、正規分布関数を用いて、一直線上の数値である「偏差値」として並べることとします。

　この作業を行うに際して、以下の「相当に乱暴な」仮説を導入することにしました。

・解析の対象は女性のみとします。男性の結婚“幸せ”データが入手できなかったためです。

・「離婚」は“不幸せ”が確定した状態であるものとし、それ以外の「結婚が継続している状態」は離婚が確定するまでは“幸せ”とみなします。数値化するためです。

・離婚率は、平成23年度の結婚件数と離婚件数の数だけを使います。ここ20年くらい結婚件数は安定移行していたので、結婚と離婚の間のタイムラグは考慮しなくても大きな問題にならないと考えたためです。

・発生確率の低い事象は、平均からの偏差が大きいとみなします。自然界の現象は概ねそのようになっているからです。方法としては、確率の大きいものから順番に正規分布の確率密度に積分することにします。

・“幸せ”と“不幸せ”は、運（ギャンブル）であるとものとします。結婚前には誰もが婚約者に対して、周到なスクリーニングを行っているはず（家柄とか、家族構成とか、相手の出身大学とか、就職先とか、趣味とかを調べること）ですが、それでも、離婚に至る夫婦が存在するという事実は、一緒に生活してみるまでは結果のわからない「サイコロの目」と同じであると考えたためです。

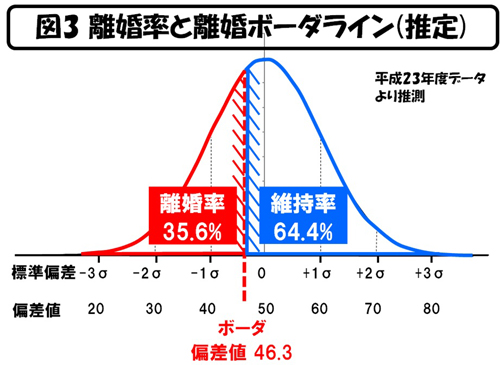
　図3は、平成23年における「結婚件数に対する離婚件数の比率、35.6％」という数値を使って、この正規分布の確率分布の積分から、離婚のボーダラインを無理矢理算出したものです（繰り返しますが、正規分布関数は、本来このような使い方をするものではありません。＜私は学生時代に、学習塾の生徒向けの成績統計解析ソフトウェアを自作していました。＞今回の手法、測定対象数を特定できず、さらに“幸せ”という本来数値で測れないものを、無理矢理数値化するために編み出した江端の独自のものです）。