60年前と今、新商品“普及の仕方”は同じか?ロジスティック曲線とバス・モデルより読み解く

新型コロナウイルス感染症の拡大が始まってから1年以上経ちました。昨年4月に寄稿した記事では「感染が指数関数的に拡大する」とはどういうことかについて書きました。そして、それはある水準で頭打ちになるので、ロジスティック関数(曲線)というシンプルな数理モデルで表されると述べました。私の専門はマーケティングですから、いったんウイルス感染の話題から離れ、新製品や新サービスを対象としたロジスティック・モデルについて事例を踏まえて話してみたいと思います。
「普及」を意味する英単語はdiffusionで、物理学などでは「拡散」と訳されます。この1年間に著しく拡散したのが新型コロナウイルスですが、それに付随してマスクを着用し社会的距離をとる行動様式も拡散=普及しました。今後についていえば、ワクチンの接種がどれだけの速度で普及するかが関心を集めそうです。望まないのに感染してしまうウイルスと違い、新しい行動様式(ニューノーマル)やワクチン接種の普及は、個人がどれだけそれを望むかに大いに依存します。したがってマーケティング・サイエンスで培われた普及モデルの知識が参考になると期待されます。
ロジスティック曲線の便利な性質
前回の記事で、感染拡大に関するロジスティック関数は
[感染者の増分] = β× [その時点までの感染者数] × [その時点の未感染者数], β > 0であると述べました。いいかえると、未感染者のうち新たに感染する人の比率は、これまでの感染者数にβという係数を掛けたものだということです。世のなかに感染者が増えるほど感染しやすくなるのは当然として、ここでは係数βを一定としている点に特徴があります(現実には政府による行動制限や自主的な行動変容が起きると、βは低下します)。もう1つ、拡散の開始時点にどれだけ感染者がいたかも加味してロジスティック曲線が描かれます(誰も感染者がいないとき、感染は広がりようがありません)。
さて、ウイルスへの感染から新製品の採用に話題を変え、新製品の普及率(累積採用率)にロジスティック曲線を当てはめることを考えます。ロジスティック曲線は係数βと開始時点での普及率を変えることで、図1のように様々な軌跡を描きます。いずれも、基本的にS字型の曲線になります。

ロジスティック曲線の便利な点は、普及率を
普及率÷(100 − 普及率)
と変換し、さらに対数変換すると(これらを合わせてロジスティック変換といいます)、図1は図2のように変わり、普及曲線が直線になることです。そしてこの直線の傾きが、もとのロジスティック関数における係数βになります。したがって、普及率のデータが得られた場合、普及率をロジスティック変換した値を縦軸に、時間を横軸にしたグラフを描き、それがほぼ直線になっていれば、ロジスティック曲線に従っていると判断できます。さらにβを知りたければ、このグラフの横軸をx、縦軸をyとする回帰分析を行い、xの回帰係数を求めればよいのです。

実際の普及率データはロジスティック曲線を描くか
では、現実の新製品・サービスの普及率はロジスティック曲線に沿って変化しているのでしょうか。図3は、1960年から2020年の期間に、いくつかの大型新製品の普及率(日本全国の2人以上世帯が対象)がどのように推移したかをグラフにしたものです。1960年代は日本の高度成長期ですが、当時3Cと呼ばれた乗用車、カラーテレビ、エアコン(その頃はクーラーと呼ばれていました)はどれもおおまかにはS字型の曲線を描いています。ただし、カラーテレビの普及は急速で、極めて短期間に普及率が100%近くまで達したことがわかります(同じことは2000年代に起きた薄型テレビの普及についてもいえます)。

ビデオカメラやパソコンの普及もS字型の曲線を描いていますが、普及率が100%近くまで行くことはなく、最近はむしろ低下気味です。これはいったん購入したが処分してしまったか、新しい世帯が購入しなくなったためでしょう。また、光ディスクやブルーレイに対応する製品は急速に普及が始まったものの、あるところで頭打ちになっています。これらの変化をロジスティック・モデルで捉えられるかどうかは、上述のように縦軸をロジスティック変換したグラフで直線になるかどうかを見ればわかります。そこで、そのような変換を施した図4を見てみましょう。

3Cといわれるカラーテレビ、自動車、エアコンでは、普及の上限に達するまでの期間について、普及率をロジスティック変換したグラフで直線を当てはめることができないわけではありません。しかし、よく眺めると時間とともに傾きが緩やかになっているようにも見えます。ビデオカメラやパソコンについては最初に傾きが小さい期間がありますが、そのうち傾きが大きくなって直線的になり、最後には小さくなっていきます。いずれについても、ロジスティック曲線が当てはまりそうな局面はありますが、すべての局面ではありません。ロジスティック関数自体が変化していくと考えると、モデルが少し複雑になります。
バス・モデルという、マーケティング・サイエンスの古典
マーケティング・サイエンスで普及データを分析するとき、ロジスティック関数よりもよく使われるのがバス・モデルです。バスとはFrank Bass というマーケティング研究者の名前で、彼が1969年に発表された論文 [1]は、その後この分野に大きな影響を与えました。ロジスティック・モデルでは新製品の採用はすべて他人の影響(過去の普及率)によって起きますが、バス・モデルでは他人の動向に関係なく起きる可能性を考慮しました。具体的にいうと、
[採用者の増分] ={p+q× [その時点の普及率] }× [その時点の未採用者数],p,q>0というのがバス・モデルです。pがあるおかげで、普及率がゼロの状態でも採用は起きます。時間が経ったときも、他人の影響を受けない採用者が未採用者から一定数現れます。そういう消費者をイノベータ(革新的採用者)と呼んでいますが、ロジャーズ[2]の定義したイノベータのように、単に採用時期が早いという意味でないことに注意して下さい(これらのモデルのより詳しい比較については、拙著[3]も参考になると思います)。他方、qはロジスティック・モデルのβと同様、世間や周囲への普及がもたらす効果を表します。
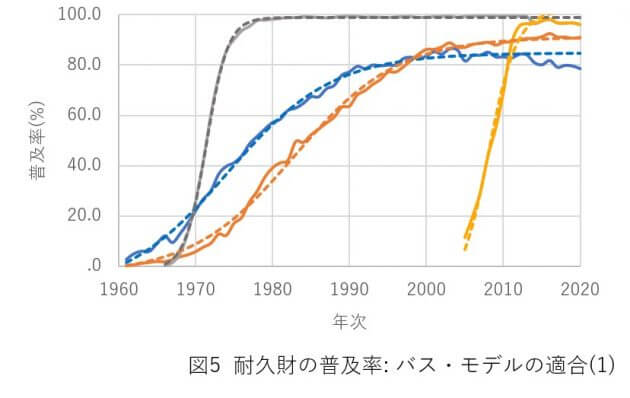
このモデルを図3で取り上げた普及データに当てはめたのが図5と図6です。実線が観測値、点線がモデルの予測値を示していますが、かなりフィットしていることがわかります(推定方法については文献[4]が参考になります)。バス・モデルは、ロジスティックス・モデルよりは柔軟に様々な普及の軌跡に当てはまります。とはいえいくつか当てはまりが悪い箇所もあります。1つは1980年代のビデオカメラ普及率、90年代のパソコン普及率です。なぜそうなったかは、市場の実態に照らして精査する必要があるでしょう。
いくつかの市場で、最近になって普及率が低下していますが、バス・モデルであれロジスティック・モデルであれ、普及率が低下する可能性は最初から考慮していません(したがってモデルの推定時には、普及率が低下した期間を含めていません)ので、そこは外して当然です。多くの普及モデルは普及率が低下する可能性を無視していますが、調査データにはそうしたケースが含まれる場合があります。製品カテゴリの衰退自体を視野に入れて分析したい場合は、その製品を処分したり、新しい世帯が採用しなかったりすることを組み入れたモデルを考える必要があるでしょう。

推定されたpとqの値は表1のようになります。そこからわかるのは、比較的最近導入された光ディスクやブルーレイの製品は他の製品よりpが大きいことです。これが、市場の急速な立ち上がりを説明している可能性があります(ただし、これらの製品については導入初期のデータがないために推定が偏ったおそれもあります)。他方、qが大きいのはカラーテレビと薄型テレビで、テレビの普及においては他者の採用の影響、あるいは「普及が普及を呼ぶ」という効果が働くと予想されます。

ワクチン接種の促進に向けて
最後に、冒頭で触れた直近の問題、たとえば新型コロナウイルスに対するワクチン接種を促進するにはどうすればいいかを考えてみましょう。いうまでもなくこの問題では、ワクチンがいつ入手可能になり、接種する体制がどれだけ整備されるかという供給側の要因が決定的に重要です。しかし、ワクチンの接種に消極的な人々がかなりの程度存在するという報道もあり、ワクチンの接種を求める需要側の要因も無視できないと思われます。そう考えると、マーケティング・サイエンスにおける普及の研究が示唆することもあるはずです。
バス・モデルが示唆するように、周囲の動向を見ながら接種するかどうかを決めるという人々が多いと、普及が急速に進むことはありません。バス・モデルのpはイノベータの効果を表していますが、要は周囲・世間の動向を気にしないで接種を行う人々が一定数必要で、そのためにメディアを使った直接的な働きかけが有効です。現時点では医療関係者への接種が先行していますが、副作用の事例だけが注目されて報道されると普及にブレーキをかけます。そうした問題を乗り越えていったん普及が始まると、他者の採用に追随するqの効果が普及を加速します。そこでは、ソーシャルメディアの役割も大きいでしょう。
そんなことは数理モデルを使わなくてもわかると思われた方もいらっしゃるでしょうが、モデルによってそのメカニズムがより明確になるはずです。
(文=水野誠/明治大学商学部教授)
<参考文献>
[1] Bass, F. M. “A New Product Growth for Model Consumer Durables,” Management Science, 15(5), 215-227, 1969. [2]エベレット・ロジャーズ『イノベーションの普及』三藤利雄訳,翔泳社、2007年。 [3]水野誠『マーケティングは進化する—クリエイティブなMarket+ingの発想』同文舘出版,2014年。 [4]里村卓也『Rで学ぶデータサイエンス13 マーケティング・モデル(第2版)』共立出版、2015年。